Thursday, October 27, 2022
Thursday, May 12, 2022
Forex Sample and Coding
ExSan++ High Perfomance C++ Computing _V22_17.2.0@05.06
iTweet#ibxsn iTweet#xsncode iTweet#xsn
FOREX TRADING My Portfolio
1 ExSan++ High Perfomance C++ Computing _V22_17.2.0@05.06
28
Trading of one currency for another with the hopes of taking advantage of small differences in conversion rates among several currencies in order to achieve a profit. For example, if 1.00 in U.S. currency buys 0.7 British pounds currency, 1.00 in British currency buys 9.5 French francs, and 1 French franc buys 0.16 in U.S. dollars, then a forex trader can start with 1.00 USD and earn 1 * 0.7 * 9.5 * 0.16 = 1.064 dollars thus earning a profit of 6.4 percent.
The problem consist to write a program that determines whether a sequence of currency exchanges can yield a profit as described above.
To result in successful trade, a sequence of exchanges must begin and end with the same currency, but any starting currency may be considered.
The input file consists of one or more conversion tables. You must solve the trading problem for each of the tables in the input file. Each table is preceded by an integer n on a line by itself giving the dimensions of the table. The maximum dimension is 20. The minimum dimension is 2.
The table then follows in row major order but with the diagonal elements of the table missing (these are assumed to have value 1.0). Thus the first row of the table represents the conversion rates between country 1 and n - 1 other countries, i.e. the amount of currency of country i constrained to 2 eq i eq n that can be purchased with one unit of the currency of country 1.
Thus each table consists of n + 1 lines in the input file: 1 line containing n and lines representing the conversion table.
Output
For each table in the input file, you must determine whether a sequence of exchanges exists that results in a profit of more than 1 percent (0.01). If a sequence exists you must print the sequence of exchanges that results in a profit. If there is more than one sequence that results in a profit of more than 1 percent you must print a sequence of minimal length, i.e. one of the sequences that uses the fewest exchanges of currencies to yield a profit.
Because the IRS (United States Internal Revenue Service) taxes long
transaction sequences with a high rate, all profitable sequences must
consist of n or fewer transactions where n is the dimension of
the table giving conversion rates. The sequence 1 2 1 represents
two conversions.
If a profitable sequence exists you must print the sequence of exchanges that results in a profit. The sequence is printed as a sequence of integers with the integer i representing the i-th line of the conversion table (country i). The first integer in the sequence is the country from which the profitable sequence starts. This integer also ends the sequence.
If no profiting sequence of n or fewer transactions exists, then the line
no trading sequence existsshould be printed.
Sample Input
3
1.2 .89
.88 5.1
1.1 0.15
4
3.1 0.0023 0.35
0.21 0.00353 8.13
200 180.559 10.339
2.11 0.089 0.06111
2
2.0
0.45Sample Output
1 2 1
1 2 4 1
no trading sequence existsAnalysis
For a given problem, the conversion table corresponds to a graph and the solution corresponds to a shortest profitable cycle in that graph. Consider the following conversion table over USD, MXN, and EUR.
3
1.004987562112089 1.004987562112089
0.99503719020999 1.004987562112089
1.004987562112089 0.99503719020999The table corresponds to the following interpretation.
| USD | MXN | EUR
----------------------------------------------
USD | 0 | 1.01^(1/2) | 1.01^(1/2)
MXN | 1.01^(-1/2) | 0 | 1.01^(1/2)
EUR | 1.01^(1/2) | 1.01^(-1/2) | 0The corresponding graph is the following.
When we interpret the conversion table, we write 0 for the rates in the diagonal to indicate that we do not consider edges that start and end in the same vertex.
The reason is that those edges are redundant.
A lasso is an edge that starts and ends in the same vertex.
Lassos are redundant because from a given sequence that includes a lasso you obtain a shorter sequence with the same rate by removing the lasso.
For example, sequence USD USD EUR USD yields profit 1.01, the same profit that the shorter sequence USD EUR USD yields.
A sequence of exchanges may yield a profit only if the sequence is a cycle.
For example, the cycle USD -> MXN -> EUR -> USD yields profit of 1.01^{3/2}.
Given that the number of vertices in the graph is 3, we do not consider cycles longer than 3.
Consider the cycles of length 3 or less.
CYCLE : RATE
USD -> MXN -> USD : 1
USD -> EUR -> USD : 1.01
EUR -> MXN -> EUR : 1
USD -> MXN -> EUR -> USD : 1.01^(3/2)
USD -> EUR -> MXN -> USD : 1.01^(-1/2)A cycle is profitable when its rate is greater or equal to 1.01. Out of the five cycles, only the following two are profitable.
USD -> EUR -> USD
USD -> MXN -> EUR -> USDOut of the two profitable cycles, USD -> EUR -> USD is the only solution because it is the shortest cycle.
A solution may not be a simple cycle like in the previous example. For example, consider the following conversion table and its corresponding graph.
4
1 0 0
1.005 0 0
0 0 0
0 0 0
For the graph, the cycles of length 4 or less are the following
CYCLE : RATE
1 2 1 : 1.005
1 2 1 2 1 : 1.010025The only profitable cycle is 1 2 1 2 1 and therefore it is the only solution.
The cycle is a solution regardless of the fact that it consists of the repetition of simple cycle 1 2 1.
A solution that is not a simple cycle is not necessarily the repetition of a simple cycle like in the previous example. For example, consider the following conversion table and its corresponding graph.
5
1.001992047666533 0 0 1.001992047666533
1.001992047666533 0 0 0
1.001992047666533 0 0 0
0 0 0 0
0 0 1.001992047666533 0
For the graph, the cycles of length 5 or less are the following.
CYCLE : RATE
1 2 1 : 1.01^(2/5)
1 5 3 1 : 1.01^(3/5)
1 2 1 5 3 1 : 1.01The only profitable cycle is 1 2 1 5 3 1 and therefore it is the only solution.
The cycle consists of simple cycles 1 2 1 and 1 5 3 1.
ExSan++ High Perfomance C++ Computing _V22_17.2.0@05.06
iTweet#ibxsn iTweet#xsncode iTweet#xsn
FOREX TRADING My Portfolio
Monday, May 9, 2022
Forex 001
| Previous Post | Next Post YET |
|---|
Exsan High Performance C++ Computing_V22_17.1.6@05.06
iTwit exsan.plusplus@gmail.com Mon May 9 13:24:34 2022 x: 18.10.25 c:\exsan JOB ID:
arbtrg2434FOREX TRADING ExSan at Work -Current Project-
Trading of one currency for another with the hopes of taking advantage of small differences in conversion rates among several currencies in order to achieve a profit. For example, if 1.00 in U.S. currency buys 0.7 British pounds currency, 1.00 in British currency buys 9.5 French francs, and 1 French franc buys 0.16 in U.S. dollars, then a forex trader can start with 1.00 USD and earn 1 * 0.7 * 9.5 * 0.16 = 1.064 dollars thus earning a profit of 6.4 percent.
The problem consist to write a program that determines whether a sequence of currency exchanges can yield a profit as described above.
To result in successful trade, a sequence of exchanges must begin and end with the same currency, but any starting currency may be considered.
The input file consists of one or more conversion tables. You must solve the trading problem for each of the tables in the input file. Each table is preceded by an integer $@n@$ on a line by itself giving the dimensions of the table. The maximum dimension is 20. The minimum dimension is 2.
The table then follows in row major order but with the diagonal elements of the table missing (these are assumed to have value 1.0). Thus the first row of the table represents the conversion rates between country 1 and $@n - 1@$ other countries, i.e. the amount of currency of country $@i@$ constrained to $@2 \leq i \leq n@$ that can be purchased with one unit of the currency of country 1.
Thus each table consists of $@n + 1@$ lines in the input file: 1 line containing $@n@$ and $@n@$ lines representing the conversion table.
Output
For each table in the input file, you must determine whether a sequence of exchanges exists that results in a profit of more than 1 percent (0.01). If a sequence exists you must print the sequence of exchanges that results in a profit. If there is more than one sequence that results in a profit of more than 1 percent you must print a sequence of minimal length, i.e. one of the sequences that uses the fewest exchanges of currencies to yield a profit.
Because the IRS (United States Internal Revenue Service) taxes long
transaction sequences with a high rate, all profitable sequences must
consist of $@n@$ or fewer transactions where $@n@$ is the dimension of
the table giving conversion rates. The sequence 1 2 1 represents
two conversions.
If a profitable sequence exists you must print the sequence of exchanges that results in a profit. The sequence is printed as a sequence of integers with the integer $@i@$ representing the $@i@$-th line of the conversion table (country $@i@$). The first integer in the sequence is the country from which the profitable sequence starts. This integer also ends the sequence.
If no profiting sequence of $@n@$ or fewer transactions exists, then the line
no trading sequence existsshould be printed.
Sample Input
3
1.2 .89
.88 5.1
1.1 0.15
4
3.1 0.0023 0.35
0.21 0.00353 8.13
200 180.559 10.339
2.11 0.089 0.06111
2
2.0
0.45Sample Output
1 2 1
1 2 4 1
no trading sequence existsAnalysis
For a given problem, the conversion table corresponds to a graph and the solution corresponds to a shortest profitable cycle in that graph. Consider the following conversion table over USD, MXN, and EUR.
3
1.004987562112089 1.004987562112089
0.99503719020999 1.004987562112089
1.004987562112089 0.99503719020999The table corresponds to the following interpretation.
| USD | MXN | EUR
----------------------------------------------
USD | 0 | 1.01^(1/2) | 1.01^(1/2)
MXN | 1.01^(-1/2) | 0 | 1.01^(1/2)
EUR | 1.01^(1/2) | 1.01^(-1/2) | 0The corresponding graph is the following.
When we interpret the conversion table, we write 0 for the rates in the diagonal to indicate that we do not consider edges that start and end in the same vertex.
The reason is that those edges are redundant.
A lasso is an edge that starts and ends in the same vertex.
Lassos are redundant because from a given sequence that includes a lasso you obtain a shorter sequence with the same rate by removing the lasso.
For example, sequence USD USD EUR USD yields profit 1.01, the same profit that the shorter sequence USD EUR USD yields.
A sequence of exchanges may yield a profit only if the sequence is a cycle.
For example, the cycle USD -> MXN -> EUR -> USD yields profit of $@1.01^{3/2}@$.
Given that the number of vertices in the graph is 3, we do not consider cycles longer than 3.
Consider the cycles of length 3 or less.
CYCLE : RATE
USD -> MXN -> USD : 1
USD -> EUR -> USD : 1.01
EUR -> MXN -> EUR : 1
USD -> MXN -> EUR -> USD : 1.01^(3/2)
USD -> EUR -> MXN -> USD : 1.01^(-1/2)A cycle is profitable when its rate is greater or equal to 1.01. Out of the five cycles, only the following two are profitable.
USD -> EUR -> USD
USD -> MXN -> EUR -> USDOut of the two profitable cycles, USD -> EUR -> USD is the only solution because it is the shortest cycle.
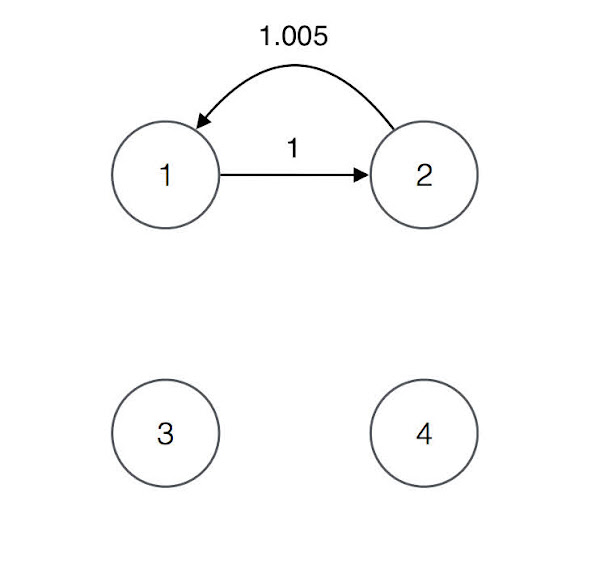
A solution may not be a simple cycle like in the previous example. For example, consider the following conversion table and its corresponding graph.
4
1 0 0
1.005 0 0
0 0 0
0 0 0
For the graph, the cycles of length 4 or less are the following
CYCLE : RATE
1 2 1 : 1.005
1 2 1 2 1 : 1.010025The only profitable cycle is 1 2 1 2 1 and therefore it is the only solution.
The cycle is a solution regardless of the fact that it consists of the repetition of simple cycle 1 2 1.
A solution that is not a simple cycle is not necessarily the repetition of a simple cycle like in the previous example. For example, consider the following conversion table and its corresponding graph.
5
1.001992047666533 0 0 1.001992047666533
1.001992047666533 0 0 0
1.001992047666533 0 0 0
0 0 0 0
0 0 1.001992047666533 0
For the graph, the cycles of length 5 or less are the following.
CYCLE : RATE
1 2 1 : 1.01^(2/5)
1 5 3 1 : 1.01^(3/5)
1 2 1 5 3 1 : 1.01The only profitable cycle is 1 2 1 5 3 1 and therefore it is the only solution.
The cycle consists of simple cycles 1 2 1 and 1 5 3 1.
Searching for a solution is difficult because there may be many cycles for a given problem. The reason is that a conversion table of length $@n@$ corresponds to complete graph $@K_n@$. Even if there are edges with weight 0, we consider them because considering a complete graph makes for a simpler solution. The exception are lassos, which we do not consider because they are redundant. For complete graphs of size $@2 \leq n \leq 20@$, the number of cycles of length $@n@$ or less is the following.
K2: 1
K3: 5
K4: 42
K5: 384
K6: 4,665
K7: 69,537
K8: 1,230,124
K9: 25,140,552
K10: 582,508,305
K11: 15,084,077,381
K12: 431,646,196,806
K13: 13,525,545,361,080
K14: 460,576,563,322,057
K15: 16,935,036,272,292,001
K16: 668,691,718,661,091,000
K17: 28,220,125,532,003,984,176
K18: 1,267,597,789,008,779,578,401
K19: 60,381,304,029,673,985,693,205
K20: 3,040,239,935,992,309,703,757,730Approach
We approach the problem by searching for a shortest profitable cycle amongst a limited number of candidates.
We guarantee that the profitable cycle we find is shortest by considering candidates in order of length.
Consider the following input graph.
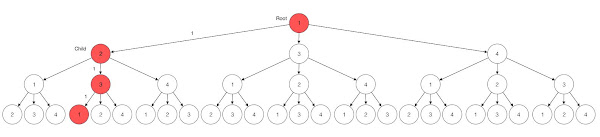
The candidates of length 2 are the cycles of length 2. Thus, we consider the cycles of length 2 from each one of the vertices as illustrated in the following diagram. These are all the cycles of length 2 because we consider all paths that start and end in each given vertex.
We search for a profitable candidate of length 2 by considering each root and each corresponding child.
For example, for root 1 and child 2, we consider the following candidate.
The rate of the candidate is 1.005 which is not profitable and therefore not a solution. We search the rest of the candidates by repeating the process for each root and child. We find no profitable candidate of length 2.
Half of the candidates of length 2 are repeated but we consider them anyway.
For example, candidate for root 2 and child 1 (2 -> 1 -> 2) is the same cycle and candidate for root 1 and child 2 (1 -> 2 -> 1).
The reason we consider repetitions is that when we apply the process to longer candidates, the number of candidates we consider for each length remains 12 while the number of cycles for the length increases.
For example, when we consider candidates of length 4 for the input graph, we consider 12 candidates instead of the 28 cycles of length 4 that exist.
Given that there is no solution of length 2, we search for a profitable candidate of length 3.
The candidates of length 3 are most beneficial cycles of length 3.
The structure of each candidate consists of a prefix edge i -> j and a suffix path j -> k -> i.
For example, the candidate for root 1 and child 2 is the following.
The prefix edge 1 -> 2 is the edge from 1 to 2 given by the input graph.
The suffix path 2 -> 3 -> 1 is a most beneficial path of length 2 from 2 to 1.
In this case the suffix is the most beneficial path of length 2 from 2 to 1.
The rate of the candidate is 1 which is not profitable and therefore not a solution.
Given that there is a candidate for each root and child, we search the rest of the candidates by repeating the process for each root and child.
We find no profitable candidate of length 3.
Candidates are most beneficial paths, for that reason we construct candidates by constructing most beneficial paths.
The construction of most beneficial paths is determined by their structure. Consider the structure a most beneficial path.
p = i -> k -> ... -> j
------------------
|
m edgesThe candidate consists of a prefix edge i -> k and a suffix path k -> ... -> j.
The suffix path is a most beneficial path of length 2 from k to j because p is a most beneficial path.
If the suffix were not most beneficial, p would not be a most beneficial path from i to j because there would be a suffix from k to j with a higher rate.
The rate B'[i,j] of path p is determined by the rate of its edge W[i,k] and the rate of its suffix B[k,j] as follows.
B'[i,j] = W[i,k] * B[k,j]The construction of a most beneficial path corresponds to the calculation of its rate.
For given origin i and destination j vertices, we obtain the rate B[m][i,j] of most beneficial path of length m from the rates of most beneficial paths of length m - 1 as follows.
B[m][i,j] = max { W[i,k] * B[m - 1][k,j] | k in 1 ... n }For the matrix of weights W corresponding to the input graph, the rate of most beneficial paths of length 1 B[1] is W.
It is possible to construct most beneficial paths on demand instead of upfront together with candidates.
We do not explain that approach because the time complexity of the end-to-end algorithm is the same either way.
We do provide an implementation of the approach for reference.
When we construct most beneficial paths, we consider many more paths than the count of candidates. While we consider 12 candidates for each length, we consider 48 paths when we compute most beneficial paths (4 roots times 3 children times 4 destination vertices). We do so because for a given input graph, the number of candidates is constant for each length and thus the total count of paths that we consider is much less than the count of cycles in the graph. Compare the overapproximation $@n^4@$ of count of paths we consider to the number of cycles in the input graph.
NUMBER OF CYCLES NUMBER OF PATHS WE CONSIDER
K2: 1 < 16
K3: 5 < 81
K4: 42 < 256
K5: 384 < 625
K6: 4,665 > 1296
K7: 69,537 > 2401
K8: 1,230,124 > 4096
K9: 25,140,552 > 6561
K10: 582,508,305 > 10000
K11: 15,084,077,381 > 14641
K12: 431,646,196,806 > 20736
K13: 13,525,545,361,080 > 28561
K14: 460,576,563,322,057 > 38416
K15: 16,935,036,272,292,001 > 50625
K16: 668,691,718,661,091,000 > 65536
K17: 28,220,125,532,003,984,176 > 83521
K18: 1,267,597,789,008,779,578,401 > 104976
K19: 60,381,304,029,673,985,693,205 > 130321
K20: 3,040,239,935,992,309,703,757,730 > 160000The overapproximation corresponds to our nested iteration of $@n@$ lengths, $@n@$ roots, $@n@$ children, and $@n@$ destination vertices.
Given that there is no solution of length 3, we search for a profitable candidate of length 4. For root 1 and child 2, the candidate is the following.
The prefix edge 1 -> 2 is given by the input graph.
The suffix path is the most beneficial path of length 3 from 2 to 1.
In this case there is only one most beneficial path, 2 1 2 1.
The rate of the candidate is 1.010025 which is profitable and thus a solution.
We stop and return the solution.
If we repeated the process for the other candidates, we would find no other solution.
Thus, 1 2 1 2 1 is the only solution.
Implementation
The following C program is the ExSan implementation of my own algorithm.
For a given weight matrix rate of size n \times n, function S executes algorithm and prints a solution if there is one.
If there is no solution, function S prints NO Sequence Exists.
EXIT FROM EXSAN
| Previous Post | Next Post YET |
|---|
Saturday, February 19, 2022
JOB: hft3106
1 ExSan++ High Perfomance C++ Computing _V22_17.1.0@11.08.a_
2 NOT VALID FOR DISTRIBUTION ---BE---careful
3 Sat Feb 19 09:31:06 2022
4
5
6 exsan.plusplus@gmail.com https://twitter.com/#!/ExSan_com
7 JOB: hft3106
8 GLUTo Sun May 15, 2022
9 License Grant for: 14 days more StockCounterDB Number of files: 7
10
11 Read From File myInvestment: 1000 Savings: 0
12
13 stFrom : 7 <---> 10000110 stTo = .77 * myInvestment / minDB : 500 / 7 I
14 pp_lastIN 0 ppnt_time 1 ppnt_data 2 ... -> prev 1, last 0
15 ... -> prev 1, last 0
16
17 stockCounterDB: 7 mu: 0.33 Limit Trading / Savings: 10000 FactoRun: 2
18 ******************
19 <--------e-x-s-a-n---------->
20 Generate Exsan ( 21 , 21 )
21
22 Total Number of assets allocated: 20
23
24 PARAMETERS
25 Investment: 1000 min Inv/Stock: 10 # Ticks -cols-: 10 beta: 0.02 ep(little ball): 0.0001
26 HedgeBand 0.45 <-- nbsp=""> 0.55 R( 0.93377 ; 0.97733 )r Lineal #Ticks: 3
27 Expected Return: 3 % minDB: 7 timesLapse: 1 timeZoomFactor: 1 retFactor: 1.5
28 Trigger Check Counter: 2 Number of times dice is thrown: 1110 EndLess: 0
29 Run: 3 onlyInteger 0 hedge: 1 ntNodes: 7 limitWeightFactor: 0.33 tickLimitToClear: 33
30 |<--------e-x-s-a-n---hft------->|
31 :1409: CHECK---- either a wrap around or no room for new data in DB geNSTOCKS: 611 nTicksLineal 3 :nTL 3
32 :1400: As it is *A ppDataIn
33 WORKSHEET 9 I[4, 10] FLOAT
34 A B C D E F G H I J
35 >----------------------------------------------------------------------<
36MSFT 1: 25.17 28.36 26.68 22.48 22.25 22.42 22.62 22.81 23.33 23.88
37TFSM 2: 71.77 69.49 69.78 70.27 71.57 69.63 68.11 68.56 68.00 65.05
38NFLX 3: 24.81 24.50 18.15 18.15 18.61 20.76 21.44 23.00 21.79 22.83
39AAPL 4: 20.52 20.32 21.89 22.69 22.07 19.98 17.34 15.06 12.35 12.68
40 <---------------------------------------------------------------------->
41 1 2 3 4 5 6 7 8 9 10
42
43 :Begin --- cluster traversal----- nStocks: 5
44 : (1, 4)-> 27.02 : (2, 1)-> 71.77 : (3, 3)-> 18.15 : (4, 1)-> 20.52 : (5, 1)-> 0.00
45 : (1, 5)-> 22.25 : (2, 2)-> 69.49 : (3, 4)-> 18.15 : (4, 2)-> 20.32 : (5, 2)-> 0.00
46 : (1, 6)-> 22.42 : (2, 3)-> 69.78 : (3, 5)-> 18.61 : (4, 3)-> 21.89 : (5, 3)-> 0.00
47 : (1, 7)-> 22.62 : (2, 4)-> 70.27 : (3, 6)-> 20.76 : (4, 4)-> 22.69 : (5, 4)-> 0.00
48 : (1, 8)-> 22.81 : (2, 5)-> 71.57 : (3, 7)-> 21.44 : (4, 5)-> 22.07 : (5, 5)-> 0.00
49 : (1, 9)-> 23.33 : (2, 6)-> 69.63 : (3, 8)-> 23.00 : (4, 6)-> 19.98 : (5, 6)-> 0.00
50 : (1, 10)-> 23.88 : (2, 7)-> 68.11 : (3, 9)-> 21.79 : (4, 7)-> 17.34 : (5, 7)-> 0.00
51 : (1, 1)-> 25.17 : (2, 8)-> 68.56 : (3, 10)-> 22.83 : (4, 8)-> 15.06 : (5, 8)-> 0.00
52 : (1, 2)-> 28.36 : (2, 9)-> 68.00 : (3, 1)-> 24.81 : (4, 9)-> 12.35 : (5, 9)-> 0.00
53 : (1, 3)-> 26.68 : (2, 10)-> 65.05 : (3, 2)-> 24.50 : (4, 10)-> 12.68 : (5, 10)-> 0.00
54
55 Data RANGE <-0 .00="" nbsp="">
56 :1589: pp_openVal
57 WORKSHEET 17 Q[4, 10] FLOAT
58 A B C D E F G H I J
59 >----------------------------------------------------------------------<
60 13 0.0000000 MSFT 1: 23.69 27.92 26.48 27.24 22.18 21.93 22.33 22.51 23.13 23.73
61 10 0.0000000 TFSM 2: 65.11 71.15 68.93 70.27 69.78 70.10 68.45 68.07 68.91 66.02
62 12 0.0000000 NFLX 3: 25.37 23.97 16.90 19.00 17.98 20.26 20.07 23.57 21.47 22.25
63 10 0.0000000 AAPL 4: 20.52 20.92 20.73 23.14 22.26 20.80 18.11 16.61 12.52 13.43
64 <---------------------------------------------------------------------->
65 1 2 3 4 5 6 7 8 9 10
66
67 :1589: pp_lowVal
68 WORKSHEET 19 S[4, 10] FLOAT
69 A B C D E F G H I J
70 >----------------------------------------------------------------------<
71 13 0.0000000 MSFT 1: 23.69 27.27 26.21 21.83 22.04 21.93 22.33 22.31 23.12 23.48
72 10 0.0000000 TFSM 2: -0.00 68.17 68.49 69.90 69.78 68.68 67.48 68.07 67.15 64.58
73 12 0.0000000 NFLX 3: 23.91 23.97 16.70 17.33 17.59 20.26 20.07 22.09 21.38 21.33
74 10 0.0000000 AAPL 4: -0.00 19.77 20.73 22.39 21.44 19.22 16.37 12.92 11.45 11.80
75 <---------------------------------------------------------------------->
76 1 2 3 4 5 6 7 8 9 10
77
78 :1589: pp_highVal
79 WORKSHEET 18 R[4, 10] FLOAT
80 A B C D E F G H I J
81 >----------------------------------------------------------------------<
82 13 0.0000000 MSFT 1: 27.50 29.09 27.14 27.24 22.62 22.70 22.89 23.21 23.63 24.46
83 10 0.0000000 TFSM 2:23325.25 71.15 71.21 70.87 72.52 70.41 69.41 68.91 69.01 66.02
84 12 0.0000000 NFLX 3: 25.50 25.27 19.60 19.00 19.78 21.13 23.17 24.38 22.20 24.67
85 10 0.0000000 AAPL 4:6668.73 20.92 23.13 23.14 22.54 20.80 18.18 17.02 14.23 13.43
86 <---------------------------------------------------------------------->
1182 :1580:End --- cluster traversal-----
Subscribe to:
Posts (Atom)